目录
快速导航-
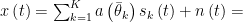
密码与信息安全 | 非均匀阵列构型设计的最新研究进展
密码与信息安全 | 非均匀阵列构型设计的最新研究进展
-
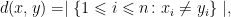
密码与信息安全 | LCDMDS码的最新研究进展
密码与信息安全 | LCDMDS码的最新研究进展
-
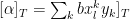
密码与信息安全 | 基于多客户端功能加密的移动群智感知系统去中心化隐私保护真相发现
密码与信息安全 | 基于多客户端功能加密的移动群智感知系统去中心化隐私保护真相发现
-
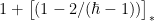
密码与信息安全 | 两类阵列族最大非周期互相关值的上界估计
密码与信息安全 | 两类阵列族最大非周期互相关值的上界估计
-
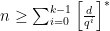
密码与信息安全 | 几类MDS码和NMDS码的构造
密码与信息安全 | 几类MDS码和NMDS码的构造
-
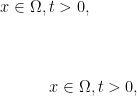
微分方程与动力系统 | 具有Dirichlet信号边界的趋化Navier-Stokes模型的整体适定性
微分方程与动力系统 | 具有Dirichlet信号边界的趋化Navier-Stokes模型的整体适定性
-
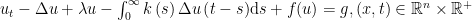
微分方程与动力系统 | 无界区域上带有记忆项的反应扩散方程全局吸引子的存在性
微分方程与动力系统 | 无界区域上带有记忆项的反应扩散方程全局吸引子的存在性
-
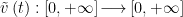
微分方程与动力系统 | 具有时滞和时间依赖阻尼的准地转方程解的稳定性
微分方程与动力系统 | 具有时滞和时间依赖阻尼的准地转方程解的稳定性
-
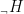
微分方程与动力系统 | Hilbert空间弱阻尼波方程周期解的存在唯一性
微分方程与动力系统 | Hilbert空间弱阻尼波方程周期解的存在唯一性
-
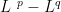
微分方程与动力系统 | 时间加权的Besov空间上带外力的分数阶Navier-Stokes方程
微分方程与动力系统 | 时间加权的Besov空间上带外力的分数阶Navier-Stokes方程
-
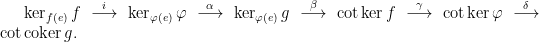
代数与逻辑模糊 | 桁架上的正合列
代数与逻辑模糊 | 桁架上的正合列
-
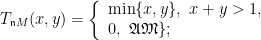
代数与逻辑模糊 | 基于三角模的不同类型的模糊隶属空间及其共轭
代数与逻辑模糊 | 基于三角模的不同类型的模糊隶属空间及其共轭
-
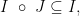
代数与逻辑模糊 | Jordan代数的三种理想的性质
代数与逻辑模糊 | Jordan代数的三种理想的性质
-
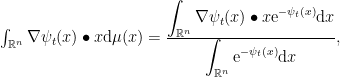
积分几何与凸分析 | Legendre对偶和 Ornstein-Uhlenbeck流
积分几何与凸分析 | Legendre对偶和 Ornstein-Uhlenbeck流
-
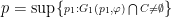
积分几何与凸分析 | 凸集的支持函数与一阶齐次函数的欧拉公式
积分几何与凸分析 | 凸集的支持函数与一阶齐次函数的欧拉公式
-
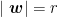
云亭青年 | 一类加权组合能量的极值问题
云亭青年 | 一类加权组合能量的极值问题
-
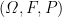
云亭青年 | 具有S-N弱鞅差序列的Hajek-Rényi型不等式及 强大数定律
云亭青年 | 具有S-N弱鞅差序列的Hajek-Rényi型不等式及 强大数定律


 与
与  的积分乘积关于时间是单调增加的.
的积分乘积关于时间是单调增加的.








 登录
登录